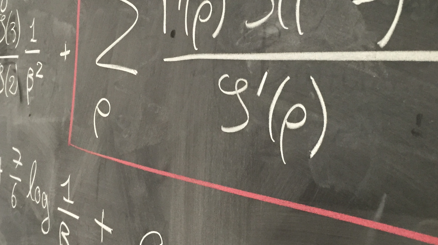Dans ce projet conjoint avec Alejandro H. Wences, nous connectons les domaines de la génétique des populations mathématique et des processus de Markov auto-similaires (AS) en dimensions infinies. Plus précisément, nous proposons un changement de perspective depuis la propriété de branchement comme paradigme dominant pour la modélisation des populations, vers une approche basée sur la propriété d’auto-similarité, que nous avons également introduite pour la première fois dans le contexte des processus stochastiques à valeurs dans l’espace des mesures positives (PVM). En étendant la transformation de Lamperti pour les processus auto-similaires au cas en dimensions infinies, nous avons pu généraliser le célèbre résultat de Birkner et al. (2005) en génétique des populations. Dans ce papier, les auteurs et autrices décrivent la généalogie de populations modélisées par un PVM de branchement alpha-stable, en termes de Beta-coalescents. Dans notre travail, nous décrivons la généalogie de populations dont la taille totale décrit un processus de Markov positif et AS en termes de n’importe quel Lambda-coalescent. Nos résultats démontrent le potentiel de la perspective de l’auto-similarité pour l’étude de modèles de populations plus complexes dans lesquels la dynamique de reproduction des individus dépend de la taille totale de la population. Parallèlement, les PVM, associés aux outils analytiques disponibles dans le domaine de la génétique des populations, comme les méthodes de dualité, constituent un modèle mathématique prometteur pour le développement de la théorie des processus de Markov AS dans le contexte des dimensions infinies.