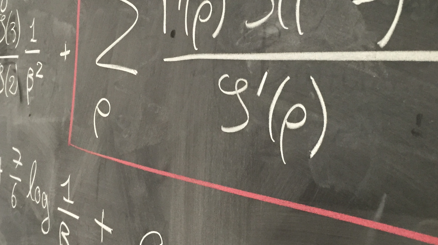Charlie Hérent
Théorème de Matsumoto-Yor à temps discret dans $SL_2$
On étudie une marche aléatoire dans le sous-groupe des matrices triangulaires inférieures de $SL_2$. On montre que l’analogue discret du processus de Matsumoto-Yor est une chaîne de Markov si et seulement si les accroissements sont distribués relativement à une loi inverse-gaussienne généralisée (GIG). Cela donne une nouvelle caractérisation de ces lois. Par ailleurs, on établit un théorème de reconstruction pour la partie diagonale de la marche relativement au processus de plus haut poids. Enfin, on étudiera la convergence de la marche vers son analogue continu.